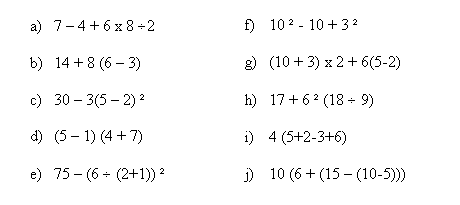
Order of Operation

Scroll down for further teaching material and practice exercises.

Video

The following rules have to be obeyed while working with mathematical equations. There is an order to how numbers are manipulated and worked on.

B E D M A S

You should memorize this acronym, as it tells you how to proceed with an equation.

B - Brackets

You must perform all mathematical calculations that occur within brackets before any other calculation in the equation.

E - Exponents

After calculations within brackets are handled, you have to perform any calculations with exponents next.

D / M - Division and Multiplication

Division and multiplication components are next. These are handled in the order they appear reading from left to right.

A / S - Addition and Subtraction

The final calculations are individual addition and subtraction questions, which are performed in the order they appear reading from left to right.

The best way to understand this process is to work through several problems.

Practice Questions

Try these practice questions to see if you are comfortable with mathematical order of operation. The final answers are listed below.

Answers

a) 27
b) 38
c) 3
d) 44
e) 71
f) 99
g) 44
h) 89
i) 40
j) 160

Grouping Like Terms

You will come across mathematical problems where you have to group like terms together. Examples of this are very common with money. Whenever you are adding sums of money, there is no need to continually restate the same denominations. Below is an example of an equation adding up a suspect’s money.

One means of calculating the total value of money seized is to individually add up all of the bills.

50 + 50 + 50 + 50 + 20 + 20 + 20 + 10 + 10 + 10 + 10

However, there is an easier and more orderly way of writing and working with this equation. Here is the statement rewritten separating the like terms.

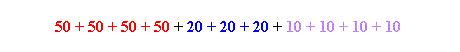
Instead of adding all of the $50 bills together you can count the number of 50’s and multiply that number by the value.

50 + 50 + 50 + 50 = 4 x 50 or 4 (50)
20 + 20 + 20 = 3 x 20 or 3 (20)
10 + 10 + 10 + 10 = 4 x 10 or 4 (10)

The statement can then be written more clearly as: 4(50) + 3 (20) + 4 (10)

Remember that it doesn’t matter what order the terms are in, so long as they remain together. The above equation could be restated any of the following ways:

3(20) + 4(50) + 4(10)
20(3) + 50(4) + 10(4)
20(3) + 10(4) + 50(4)
4(10) + 3(20) + 4(50)

Like terms can occur in any addition question. It doesn’t have to be a monetary question. Any time you see two or more of the same number in an addition problem, they can be combined.

5 + 6 + 3 + 5 + 2 + 6 + 5 = 3(5) + 2(6) + 3 + 2
75 + 63 + 75 + 63 + 75 = 3(75) + 2(63)
5 + 5 + 5 + 5 + 5 + 4 = 5(5) + 4